Тригонометрическая подстановка

В математике тригонометрическая подстановка — это подстановка из тригонометрических функций для других выражений. В исчислении тригонометрическая подстановка — это метод вычисления интегралов. Более того, можно использовать тригонометрические тождества для упрощения некоторых интегралов, содержащих радикальное выражение. Как и другие методы интегрирования путём подстановки, при вычислении определённого интеграла может быть проще полностью вывести первообразную перед применением границ интегрирования.

Случай I: Подынтегральные выражения, содержащие a² − x²

Пусть [math]\displaystyle{ x = a \sin \theta }[/math], и используйте тождество [math]\displaystyle{ 1-\sin^2 \theta = \cos^2 \theta }[/math].

Примеры Случая I

Геометрическая конструкция для Случая I

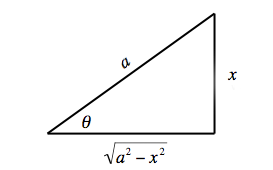
Пример 1

В интеграле

[math]\displaystyle{ \int\frac{dx}{\sqrt{a^2-x^2}}, }[/math]

можно использовать

[math]\displaystyle{ x=a\sin \theta,\quad dx=a\cos\theta\, d\theta, \quad \theta=\arcsin\frac{x}{a}. }[/math]

Тогда

[math]\displaystyle{ \begin{align} \int\frac{dx}{\sqrt{a^2-x^2}} &= \int\frac{a\cos\theta \,d\theta}{\sqrt{a^2-a^2\sin^2 \theta}} \\[6pt] &= \int\frac{a\cos\theta\,d\theta}{\sqrt{a^2(1 - \sin^2 \theta )}} \\[6pt] &= \int\frac{a\cos\theta\,d\theta}{\sqrt{a^2\cos^2\theta}} \\[6pt] &= \int d\theta \\[6pt] &= \theta + C \\[6pt] &= \arcsin\frac{x}{a}+C. \end{align} }[/math]

Вышеупомянутый шаг требует, чтобы [math]\displaystyle{ a \gt 0 }[/math] и [math]\displaystyle{ \cos \theta \gt 0 }[/math]. Мы можем выбрать [math]\displaystyle{ a }[/math] в качестве главного корня [math]\displaystyle{ a^2 }[/math] и наложить ограничение [math]\displaystyle{ -\pi /2 \lt \theta \lt \pi /2 }[/math] с помощью функции обратного синуса.

Для определённого интеграла нужно выяснить, как меняются границы интегрирования. Например, если [math]\displaystyle{ x }[/math] изменяется от [math]\displaystyle{ 0 }[/math] до [math]\displaystyle{ a/2 }[/math], тогда [math]\displaystyle{ \sin \theta }[/math] изменяется от [math]\displaystyle{ 0 }[/math] до [math]\displaystyle{ 1/2 }[/math], поэтому [math]\displaystyle{ \theta }[/math] изменяется от [math]\displaystyle{ 0 }[/math] до [math]\displaystyle{ \pi / 6 }[/math]. Тогда

[math]\displaystyle{ \int_0^{a/2}\frac{dx}{\sqrt{a^2-x^2}}=\int_0^{\pi/6} d\theta = \frac{\pi}{6}. }[/math]

При выборе границ требуется некоторая осторожность. Поскольку приведённая выше интеграция требует, чтобы [math]\displaystyle{ -\pi /2 \lt \theta \lt \pi /2 }[/math], значение [math]\displaystyle{ \theta }[/math] может изменяться только от [math]\displaystyle{ 0 }[/math] до [math]\displaystyle{ \pi / 6 }[/math]. Пренебрегая этим ограничением, можно было бы выбрать [math]\displaystyle{ \theta }[/math] для перехода от [math]\displaystyle{ \pi }[/math] к [math]\displaystyle{ 5\pi /6 }[/math], что привело бы фактически к отрицательному значению.

В качестве альтернативы можно полностью вычислить неопределённые интегралы перед применением граничных условий. В этом случае первообразная даёт

[math]\displaystyle{ \int_{0}^{a/2} \frac{dx}{\sqrt{a^2 - x^2}} = \arcsin \left( \frac{x}{a} \right) \Biggl|_{0}^{a/2} = \arcsin \left ( \frac{1}{2}\right) - \arcsin (0) = \frac{\pi}{6} }[/math]

как прежде.

Пример 2

Интеграл

[math]\displaystyle{ \int\sqrt{a^2-x^2}\,dx, }[/math]

можно оценить путём представления [math]\displaystyle{ x=a\sin \theta,\, dx=a\cos\theta\, d\theta,\, \theta=\arcsin\frac{x}{a}, }[/math]

где [math]\displaystyle{ a \gt 0 }[/math], так что [math]\displaystyle{ \sqrt{a^2}=a }[/math] и [math]\displaystyle{ -\frac{\pi}{2} \le \theta \le \frac{\pi}{2} }[/math] по диапазону арксинуса, так что [math]\displaystyle{ \cos \theta \ge 0 }[/math] и [math]\displaystyle{ \sqrt{\cos^2 \theta} = \cos \theta }[/math].

Тогда

[math]\displaystyle{ \begin{align} \int\sqrt{a^2-x^2}\,dx &= \int\sqrt{a^2-a^2\sin^2\theta}\,(a\cos\theta) \,d\theta \\[6pt] &= \int\sqrt{a^2(1-\sin^2\theta)}\,(a\cos\theta) \,d\theta \\[6pt] &= \int\sqrt{a^2(\cos^2\theta)}\,(a\cos\theta) \,d\theta \\[6pt] &= \int(a\cos\theta)(a\cos\theta) \,d\theta \\[6pt] &= a^2\int\cos^2\theta\,d\theta \\[6pt] &= a^2\int\left(\frac{1+\cos 2\theta}{2}\right)\,d\theta \\[6pt] &= \frac{a^2}{2} \left(\theta+\frac{1}{2}\sin 2\theta \right) + C \\[6pt] &= \frac{a^2}{2}(\theta+\sin\theta\cos\theta) + C \\[6pt] &= \frac{a^2}{2}\left(\arcsin\frac{x}{a}+\frac{x}{a}\sqrt{1-\frac{x^2}{a^2}}\right) + C \\[6pt] &= \frac{a^2}{2}\arcsin\frac{x}{a}+\frac{x}{2}\sqrt{a^2-x^2}+C. \end{align} }[/math]

Для определённого интеграла границы изменяются после выполнения замены и определяются с помощью уравнения [math]\displaystyle{ \theta = \arcsin\frac{x}{a} }[/math] со значениями в диапазоне [math]\displaystyle{ -\frac{\pi}{2} \le \theta \le \frac{\pi}{2} }[/math]. Или же можно применить граничные члены непосредственно к формуле первообразной.

Например, определённый интеграл

[math]\displaystyle{ \int_{-1}^1\sqrt{4-x^2}\,dx, }[/math]

можно оценить, подставив [math]\displaystyle{ x = 2\sin\theta, \,dx = 2\cos\theta\,d\theta }[/math], с оценками, определёнными с помощью [math]\displaystyle{ \theta = \arcsin\frac{x}{2} }[/math], [math]\displaystyle{ \arcsin(1/2) = \pi/6 }[/math] и [math]\displaystyle{ \arcsin(-1/2) = -\pi/6 }[/math].

Тогда

[math]\displaystyle{ \begin{align} \int_{-1}^1\sqrt{4-x^2}\,dx &= \int_{-\pi/6}^{\pi/6}\sqrt{4-4\sin^2\theta}\,(2\cos\theta) \,d\theta \\[6pt] &= \int_{-\pi/6}^{\pi/6}\sqrt{4(1-\sin^2\theta)}\,(2\cos\theta) \,d\theta \\[6pt] &= \int_{-\pi/6}^{\pi/6}\sqrt{4(\cos^2\theta)}\,(2\cos\theta) \,d\theta \\[6pt] &= \int_{-\pi/6}^{\pi/6}(2\cos\theta)(2\cos\theta) \,d\theta \\[6pt] &= 4\int_{-\pi/6}^{\pi/6}\cos^2\theta\,d\theta \\[6pt] &= 4\int_{-\pi/6}^{\pi/6}\left(\frac{1+\cos 2\theta}{2}\right)\,d\theta \\[6pt] &= 2 \left[\theta+\frac{1}{2} \sin 2\theta \right]^{\pi/6}_{-\pi/6} = [2\theta+\sin 2\theta] \Biggl |^{\pi/6}_{-\pi/6} \\[6pt] &= \left(\frac{\pi}{3}+\sin\frac{\pi}{3}\right)-\left(-\frac{\pi}{3}+\sin\left(-\frac{\pi}{3}\right)\right) = \frac{2\pi}{3}+\sqrt{3}. \end{align} }[/math]

С другой стороны, прямое применение граничных членов к ранее полученной формуле для первообразных даёт

[math]\displaystyle{ \begin{align} \int_{-1}^1\sqrt{4-x^2}\,dx &= \left[ \frac{2^2}{2}\arcsin\frac{x}{2}+\frac{x}{2}\sqrt{2^2-x^2} \right]_{-1}^{1}\\[6pt] &= \left( 2 \arcsin \frac{1}{2} + \frac{1}{2}\sqrt{4-1}\right) - \left( 2 \arcsin \left(-\frac{1}{2}\right) + \frac{-1}{2}\sqrt{4-1}\right)\\[6pt] &= \left( 2 \cdot \frac{\pi}{6} + \frac{\sqrt{3}}{2}\right) - \left( 2\cdot \left(-\frac{\pi}{6}\right) - \frac{\sqrt 3}{2}\right)\\[6pt] &= \frac{2\pi}{3} + \sqrt{3} \end{align} }[/math]

как прежде.

Случай II: Подынтегральные выражения, содержащие a² + x²

Примеры Случая II

Геометрическая конструкция для Случая II

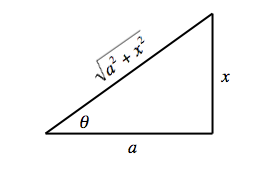
Пример 1

В интеграле

[math]\displaystyle{ \int\frac{dx}{a^2+x^2} }[/math]

можно написать

[math]\displaystyle{ x=a\tan\theta,\quad dx=a\sec^2\theta\, d\theta, \quad \theta=\arctan\frac{x}{a}, }[/math]

так что интеграл становится

[math]\displaystyle{ \begin{align} \int\frac{dx}{a^2+x^2} &= \int\frac{a\sec^2\theta\, d\theta}{a^2 + a^2\tan^2\theta} \\[6pt] &= \int\frac{a\sec^2\theta\, d\theta}{a^2(1+\tan^2\theta)} \\[6pt] &= \int\frac{a\sec^2\theta\, d\theta}{a^2\sec^2\theta} \\[6pt] &= \int\frac{d\theta}{a} \\[6pt] &= \frac{\theta}{a}+C \\[6pt] &= \frac{1}{a} \arctan \frac{x}{a} + C, \end{align} }[/math]

при условии [math]\displaystyle{ a \neq 0 }[/math].

Для определённого интеграла границы изменяются после выполнения замены и определяются с помощью уравнения [math]\displaystyle{ \theta = \arctan\frac{x}{a} }[/math] со значениями в диапазоне [math]\displaystyle{ -\frac{\pi}{2} \lt \theta \lt \frac{\pi}{2} }[/math]. Или же можно применить граничные члены непосредственно к формуле первообразной.

Например, определённый интеграл

[math]\displaystyle{ \int_0^1\frac{4}{1+x^2}\,dx }[/math]

можно оценить, подставив [math]\displaystyle{ x = \tan\theta, \,dx = \sec^2\theta\,d\theta }[/math], с оценками, определёнными с помощью [math]\displaystyle{ \theta = \arctan x }[/math], [math]\displaystyle{ \arctan 0 = 0 }[/math] и [math]\displaystyle{ \arctan 1 = \pi/4 }[/math].

Тогда

[math]\displaystyle{ \begin{align} \int_0^1\frac{4\,dx}{1+x^2} &= 4\int_0^1\frac{dx}{1 + x^2} \\[6pt] &= 4\int_0^{\pi/4}\frac{\sec^2\theta\, d\theta}{1+\tan^2\theta} \\[6pt] &= 4\int_0^{\pi/4}\frac{\sec^2\theta\, d\theta}{\sec^2\theta} \\[6pt] &= 4\int_0^{\pi/4}d\theta \\[6pt] &= (4\theta)\Bigg|^{\pi/4}_0 = 4 \left (\frac{\pi}{4} - 0 \right) = \pi. \end{align} }[/math]

Между тем, прямое применение граничных членов к формуле для первообразных даёт

[math]\displaystyle{ \begin{align} \int_0^1\frac{4}{1+x^2}\,dx &= 4\int_0^1\frac{dx}{1+x^2} \\ &= 4\left[\frac{1}{1} \arctan \frac{x}{1} \right]^1_0 \\ &= 4(\arctan x)\Bigg|^1_0 \\ &= 4(\arctan 1 - \arctan 0) \\ &= 4 \left (\frac{\pi}{4} - 0 \right) = \pi, \end{align} }[/math]

так же, как прежде.

Пример 2

Интеграл

[math]\displaystyle{ \int\sqrt{a^2+x^2}\,{dx} }[/math]

можно оценить путём представления [math]\displaystyle{ x=a\tan\theta,\, dx=a\sec^2\theta\, d\theta, \, \theta=\arctan\frac{x}{a}, }[/math]

где [math]\displaystyle{ a \gt 0 }[/math], так что [math]\displaystyle{ \sqrt{a^2}=a }[/math] и [math]\displaystyle{ -\frac{\pi}{2}\lt \theta\lt \frac{\pi}{2} }[/math] по диапазону арктангенса, так что [math]\displaystyle{ \sec \theta \gt 0 }[/math] и [math]\displaystyle{ \sqrt{\sec^2 \theta} = \sec \theta }[/math].

Тогда

[math]\displaystyle{ \begin{align} \int\sqrt{a^2+x^2}\,dx &= \int\sqrt{a^2 + a^2\tan^2\theta}\,(a \sec^2\theta)\, d\theta \\[6pt] &= \int\sqrt{a^2 (1+\tan^2\theta)}\,(a \sec^2\theta)\, d\theta \\[6pt] &= \int\sqrt{a^2 \sec^2\theta}\,(a \sec^2\theta)\, d\theta \\[6pt] &= \int(a \sec\theta)(a \sec^2\theta)\, d\theta \\[6pt] &= a^2\int \sec^3\theta\, d\theta. \\[6pt] \end{align} }[/math]

Интеграл секанса в кубе можно вычислить с помощью интегрирования по частям. Как результат

[math]\displaystyle{ \begin{align} \int\sqrt{a^2+x^2}\,dx &= \frac{a^2}{2}(\sec\theta \tan\theta + \ln|\sec\theta+\tan\theta|)+C \\[6pt] &= \frac{a^2}{2}\left(\sqrt{1+\frac{x^2}{a^2}}\cdot\frac{x}{a} + \ln\left|\sqrt{1+\frac{x^2}{a^2}}+\frac{x}{a}\right|\right)+C \\[6pt] &= \frac{1}{2}\left(x\sqrt{a^2+x^2} + a^2\ln\left|\frac{x+\sqrt{a^2+x^2}}{a}\right|\right)+C. \end{align} }[/math]

Случай III: Подынтегральные выражения, содержащие x² − a²

Пусть [math]\displaystyle{ x = a \sec \theta }[/math] и используется тождество [math]\displaystyle{ \sec^2 \theta -1 = \tan^2 \theta. }[/math]

Примеры Случая III

Геометрическая конструкция для Случая III

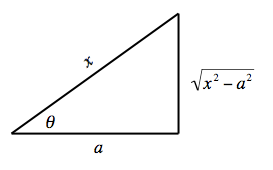
Интегралы типа

[math]\displaystyle{ \int\frac{dx}{x^2 - a^2} }[/math]

также можно вычислить частичными дробями, а не тригонометрическими подстановками. Однако интеграл

[math]\displaystyle{ \int\sqrt{x^2 - a^2}\, dx }[/math]

нельзя. В этом случае подходящей подстановкой будет:

[math]\displaystyle{ x = a \sec\theta,\, dx = a \sec\theta\tan\theta\, d\theta, \, \theta = \arcsec\frac{x}{a}, }[/math]

где [math]\displaystyle{ a \gt 0 }[/math], так что [math]\displaystyle{ \sqrt{a^2}=a }[/math] и [math]\displaystyle{ 0 \le \theta \lt \frac{\pi}{2} }[/math], предполагая [math]\displaystyle{ x \gt 0 }[/math], так что [math]\displaystyle{ \tan \theta \ge 0 }[/math] и [math]\displaystyle{ \sqrt{\tan^2 \theta} = \tan \theta }[/math].

Тогда

[math]\displaystyle{ \begin{align} \int\sqrt{x^2 - a^2}\, dx &= \int\sqrt{a^2 \sec^2\theta - a^2} \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int\sqrt{a^2 (\sec^2\theta - 1)} \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int\sqrt{a^2 \tan^2\theta} \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int a^2 \sec\theta\tan^2\theta\, d\theta \\ &= a^2 \int (\sec\theta)(\sec^2\theta - 1)\, d\theta \\ &= a^2 \int (\sec^3\theta - \sec\theta)\, d\theta. \end{align} }[/math]

Можно вычислить интеграл функции секанс, умножив числитель и знаменатель на [math]\displaystyle{ ( \sec \theta + \tan \theta) }[/math] и интеграл секанса в кубе по частям. Как результат

[math]\displaystyle{ \begin{align} \int\sqrt{x^2-a^2}\,dx &= \frac{a^2}{2}(\sec\theta \tan\theta + \ln|\sec\theta+\tan\theta|)-a^2\ln|\sec\theta+\tan\theta|+C \\[6pt] &= \frac{a^2}{2}(\sec\theta \tan\theta - \ln|\sec\theta+\tan\theta|)+C \\[6pt] &= \frac{a^2}{2}\left(\frac{x}{a}\cdot\sqrt{\frac{x^2}{a^2}-1} - \ln\left|\frac{x}{a}+\sqrt{\frac{x^2}{a^2}-1}\right|\right)+C \\[6pt] &= \frac{1}{2}\left(x\sqrt{x^2-a^2} - a^2\ln\left|\frac{x+\sqrt{x^2-a^2}}{a}\right|\right)+C. \end{align} }[/math]

Если [math]\displaystyle{ \frac{\pi}{2} \lt \theta \le \pi }[/math], что происходит, когда [math]\displaystyle{ x \lt 0 }[/math] с заданным диапазоном арксеканса, то [math]\displaystyle{ \tan \theta \le 0 }[/math], что в данном случае означает [math]\displaystyle{ \sqrt{\tan^2 \theta} = -\tan \theta }[/math].

Подстановки, исключающие тригонометрические функции

Подстановка может использоваться для удаления тригонометрических функций.

Например,

[math]\displaystyle{ \begin{align} \int f(\sin(x), \cos(x))\, dx &=\int\frac1{\pm\sqrt{1-u^2}} f\left(u,\pm\sqrt{1-u^2}\right)\, du && u=\sin (x) \\[6pt] \int f(\sin(x), \cos(x))\, dx &=\int\frac{1}{\mp\sqrt{1-u^2}} f\left(\pm\sqrt{1-u^2},u\right)\, du && u=\cos (x) \\[6pt] \int f(\sin(x), \cos(x))\, dx &=\int\frac2{1+u^2} f \left(\frac{2u}{1+u^2},\frac{1-u^2}{1+u^2}\right)\, du && u=\tan\left (\tfrac{x}{2} \right ) \\[6pt] \end{align} }[/math]

Последняя подстановка известна как подстановка Вейерштрасса, в которой используются формулы тангенса половинного угла.

Например,

[math]\displaystyle{ \begin{align} \int\frac{4 \cos x}{(1+\cos x)^3}\, dx &= \int\frac2{1+u^2}\frac{4\left(\frac{1-u^2}{1+u^2}\right)}{\left(1+\frac{1-u^2}{1+u^2}\right)^3}\, du = \int (1-u^2)(1+u^2)\, du \\&= \int (1-u^4)\,du = u - \frac{u^5}{5} + C = \tan \frac{x}{2} - \frac{1}{5} \tan^5 \frac{x}{2} + C. \end{align} }[/math]

Гиперболическая подстановка

Подстановки гиперболических функций также могут использоваться для упрощения интегралов.

В интеграле [math]\displaystyle{ \int \frac{1}{\sqrt{a^2+x^2}}\, dx }[/math] можно сделать подстановку [math]\displaystyle{ x=a\sinh{u} }[/math], [math]\displaystyle{ dx=a\cosh u\, du. }[/math]

Затем, используя тождества [math]\displaystyle{ \cosh^2 (x) - \sinh^2 (x) = 1 }[/math] и [math]\displaystyle{ \sinh^{-1}{x} = \ln(x + \sqrt{x^2 + 1}), }[/math]

можно получить

[math]\displaystyle{ \begin{align} \int \frac{1}{\sqrt{a^2+x^2}}\, dx &= \int \frac{a\cosh u}{\sqrt{a^2+a^2\sinh^2 u}}\, du\\[6pt] &=\int \frac{a\cosh{u}}{a\sqrt{1+\sinh^2{u}}}\, du\\[6pt] &=\int \frac{a\cosh{u}}{a\cosh u}\, du\\[6pt] &=u+C\\[6pt] &=\sinh^{-1}{\frac{x}{a}}+C\\[6pt] &=\ln\left(\sqrt{\frac{x^2}{a^2} + 1} + \frac{x}{a}\right) + C\\[6pt] &=\ln\left(\frac{\sqrt{x^2+a^2} + x}{a}\right) + C. \end{align} }[/math]

См. также

• Универсальная тригонометрическая подстановка
• Подстановки Эйлера